ゼロから作るDeep Learningとともに学ぶフレームワーク(学習テクニック編)
はじめに
このシリーズでは、深層学習の入門書として有名な、「ゼロから作るDeep Learning」(以下、ゼロから〜)と同時並行で、フレームワークを学習し、その定着を目指します。
前回までは、Kerasを活用して実際にニューラルネットワークを学習させて、そのモデルを活用して推論までできるようになりました。今回は、ゼロから〜の6章に対応する種々の学習テクニックについて扱います。幅広いトピックを扱うので、理解するのに時間がかかるかと思いますが、どれもモデルの性能と安定性を向上させるために、重要なものばかりです。したがって、一つ一つ理解できるまでじっくりと取り組むことをオススメします。
それでは、まずはパラメータの最適化アルゴリズムについての話題から入っていきましょう!
1. 最適化アルゴリズム
ゼロから〜で紹介があったように、ニューラルネットワークに対して適用される最適化アルゴリズムはたくさん存在し、モデルに応じて使い分けることが、その性能を引き出すために非常に重要となります。
ここでは、ゼロから〜のP177に登場した、「SGD、AdaGrad、Adam」に加え、Adadelta、Nadam、の5つの最適化アルゴリズムを、Fashion-MNISTデータセットの分類実験を通して、比較してみようと思います。
1.1 Fashion-MNISTデータセット
本稿で用いるFashion-MNISTデータセットは、MNISTデータセットと互換性のあるデータセットです。データセットの内容は手書き数字ではなく、靴やズボン、カバン、服などファッションに関係のあるものとなっています。
Fashion-MNISTは、MNISTの分類タスクが「簡単過ぎること」などを理由に、それを置き換える目的で作成されたデータセットです。
試しに1枚データセットの画像を表示させてみましょう。下記のソースコードを動作させてみてください。画像の表示は、imshowメソッドを使えば簡単にできます。
from keras.datasets import fashion_mnist
import matplotlib.pyplot as plt
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
plt.figure()
plt.imshow(x_train[0], cmap='gray')
plt.show()
Output:
靴らしき画像が表示されているのが確認できますね。
参考: (Fashion-MNISTのGitHubレポジトリ )
参考: (KerasにおけるFashion-MNISTデータセットの説明)
1.2 モデルの実装
本実験に用いるモデルの構造とハイパーパラメータは、ゼロから〜の公式レポジトリにあるソースコードに基づきます。実装自体は前回までのソースコードをほぼ流用して実現できるので、ここでは説明を省略します。ソースコード自体は、GitHubのcompare_optimizer.pyにて公開してあります。
なお、自力で実装をしてみたい方は、公式レポジトリを見つつ、前回のソースコードをベースにすることをおすすめします。
参照: ゼロから〜のP176〜P178
参照: (GitHub: compare_optimizer.py)
参照: (Kerasで利用可能な最適化アルゴリズムについて)
1.3 モデルの比較
1.2で実装した5層ニューラルネットワークを実行させると、以下のような結果が得られました。
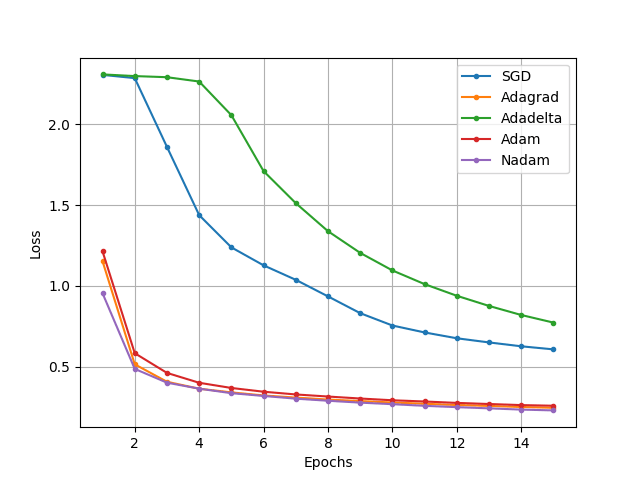
図から、SGDとAdadeltaを用いたモデルは、Adam/Nadam/Adagradを用いたモデルよりも収束が遅いことがわかります。また、この実験においては、Nadamが5つの最適化アルゴリズムの中で、最も収束の速いアルゴリズムであることがわかりました。
2. 重みの初期化
Kerasにおける重みの初期化は特に指定しない限り、ブラックボックス的に処理されます。つまり、レイヤー定義時に重みの初期化方法を指定しなければ、各層の所定の初期化方法が自動的に適用されます。
ここでは、重みの初期化をこちらから事前に指定することで、フレームワーク(Keras)を活用したときの、初期化手法による収束速度の違いを検証していきます。
2.1 公式ドキュメントを見てみる
ここで、全結合層: Denseレイヤーの公式ドキュメントを確認してみましょう。下記がドキュメントの一部抜粋になります。
keras.layers.Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform',
kernel_initializerを見ると、初期化の手法として、Glorotの一様分布(Xavierの一様分布)が用いられていることがわかります。
初期化手法を変更したい場合には、すでに定義されている手法をkernel_initializerに引数として与えるか、新たに手法自体を定義することもできます。新たに定義する方法については、公式ドキュメントをご覧ください。
参照: (KerasにおけるDenseレイヤーのドキュメント)
参照: (Kerasにおける初期化手法についてのドキュメント)
2.2 初期化手法による収束速度の違い
では、前章で実装した5層ニューラルネットワークを活用して、初期化手法による収束速度の違いをKerasでも検証していきましょう。
初期化手法には、デフォルトのXaiverの初期値とHeの初期値、標準偏差が0.01の正規分布の3つをそれぞれ用います。また、ゼロから〜のP184〜P186の実験設定と合わせるため、中間層の活性化関数をsigmoidからreluに変更します。ソースコードは、GitHubのcompare_initializer.pyより入手できます。
compare_initializer.pyを動作させた結果、以下の図のような結果が得られました。
Output:
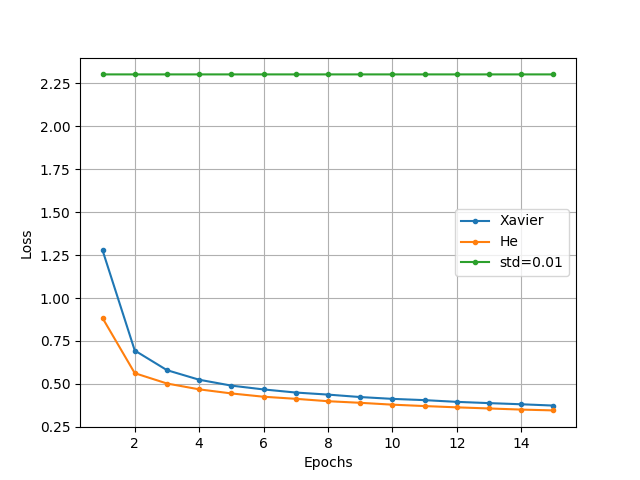
図より、やはり活性化関数にReLUを用いる場合には、Heの一様分布による初期化が最も適していることがわかりました。
参考: ゼロから〜のP184〜P186
参照: (GitHub: compare_initializer.py)
3. 正規化・正則化
以下、4章と5章では、それぞれ正規化と正則化について扱います。その前に、巷で誤用しがちな、機械学習における正規化と正則化の意味について確認しておきましょう。
3.1 正規化
機械学習における正規化は、「データをある範囲内にスケールすること」を意味します。標準化とも呼ばれることがありますが、標準化と正規化では厳密には意味合いが異なります。標準化: standardization は、「平均が0、分散が1」になるようにデータをスケールすることを指します。なお、この用語は統計学で用いられることが多いようです。
したがって、正規化は標準化を抽象化したような意味合いを持ちます。
3.2 正則化
正則化は過学習(過適応)を防ぐためにある種のペナルティを課すことを意味します。Weight Decayがその一例となります。
4. バッチ正規化
バッチ正規化は、入力データを平均値が0で分散が1となる分布に変換する手法のことを指します。バッチ正規化を適用することで、モデルの収束を高速化できるほか、重みの初期化手法に対してかなり頑健になります。
では、Kerasでバッチ正規化の実験をしてみましょう。
4.1 モデルの実装
Kerasにおいて、バッチ正規化はBatchNormalizationレイヤーを活用することで実装できます。
ここでは、2章のモデルの「全結合層と活性化層の間」にバッチ正規化層を追加する形で実装します。また、重みの初期化は「標準偏差が0.01の正規分布」により行います。
なお、2章で確認したように、この重み初期化では通常学習は全く進行しません。つまり、バッチ正規化を適用することで、どの程度初期化手法に対して頑健になるかを見てみます。
Kerasにおけるバッチ正規化の適用例は以下のようになります。
_hidden = Dense(hidden_dim, kernel_initializer=_init)(_hidden)
_hidden = BatchNormalization()(_hidden)
_hidden = Activation('relu')(_hidden)
ソースコードは、GitHubより入手できます。
参照: (KerasにおけるBatch Normalizationについて)
参照: (GitHub: compare_batch_norm.py)
4.2 バッチ正規化の有無による分類精度の比較
compare_batch_norm.pyを動作させた結果、以下の図のような結果が得られました。
Output:
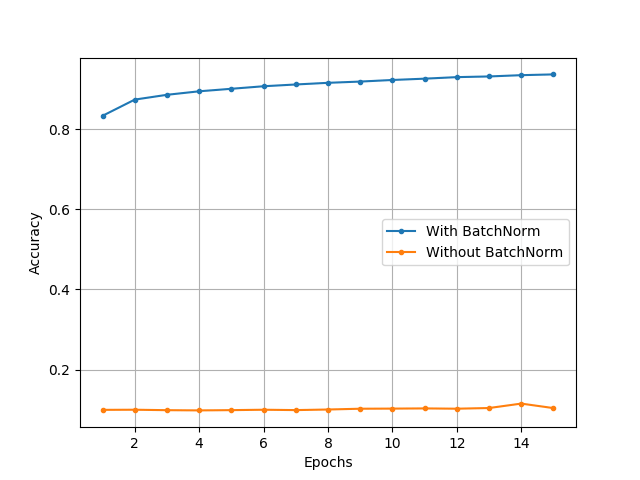
図より、バッチ正規化をモデルに適用することで、かなり適当な重みの初期化を行っても、きちんと学習してくれることがわかります!
参考: ゼロから〜のP186〜P189
5. 過学習を防ぐためのテクニック
ここでは、過学習を防ぐための手法の一例として、ゼロから〜でも扱われていた、Weight decayとドロップアウトに加え、Early Stoppingついても扱います。前章までと同様にKerasでテストモデルを実装し、それぞれの手法の効果を検証します。
5.1 Weight decay
5.1.1 KerasにおけるWeight decayの適用方法
KerasにおけるWeight decayは、各レイヤーの引数に存在する、kernel_regularizerに対して利用したい正則化手法を与えることで利用できます。
ここでは、4章で実装したバッチ正規化ありのモデルにweight decayを適用することで、過学習が軽減するか検証していきます。
Weight decayの簡単な適用例は以下のようになります。
from keras import regularizers
_wd = regularizers.l2(0.1)
_hidden = Dense(hidden_dim, kernel_initializer=_init, kernel_regularizer=_wd)(_hidden)
ソースコードは、GitHubにある、compare_weight_decay.pyとなります。
参考: (Kerasにおける正則化の利用方法について)
参照: (GitHub: compare_weight_decay.py)
5.1.2 Weight decayの適用結果
compare_weight_decay.pyを動作させた結果、以下のような図が得られました。
Output:
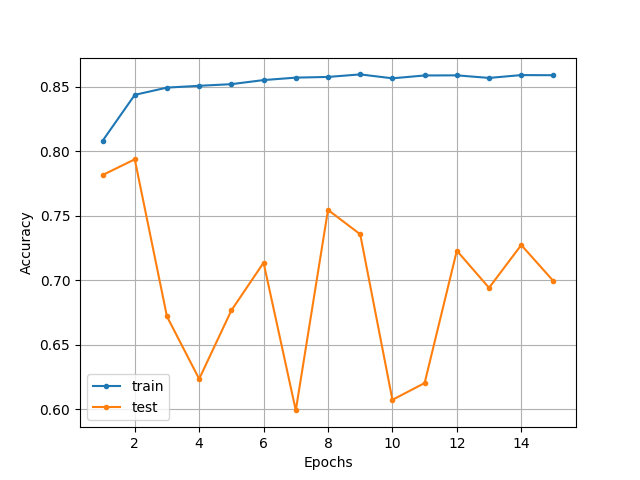
<Weight decayありのときの分類精度の推移>
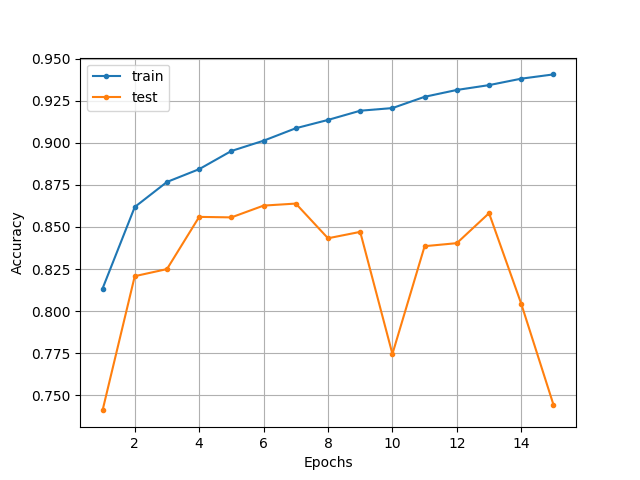
<Weight decayなしのときの分類精度の推移>
図より、Weigth decayの有無を問わず、テスト精度はかなり乱高下していることがわかります。一方で、訓練精度については、Weight decayを用いることで、過学習が抑制されていることがわかります。
5.2 ドロップアウト
5.2.1 ドロップアウトの実装
Kerasにおいて、ドロップアウトはDropoutレイヤーを活用することで実装できます。
ドロップアウトの適用例は以下のようになります。
下記の例では、ドロップアウト率(入力のユニットを消去する割合)を、引数: rateに渡しています。
_hidden = Dense(hidden_dim, activation='relu')(_hidden)
_hidden = Dropout(rate=dpout_rate)(_hidden)
5層ニューラルネットワークでドロップアウトの効果を検証したソースコードは、compare_dropout.pyとして、GitHubに置いてあります。では、この実験結果について次項で見ていきます。
5.2.2 ドロップアウトの適用結果
compare_dropout.pyを動作させた結果、以下のような図が得られました。
Output:
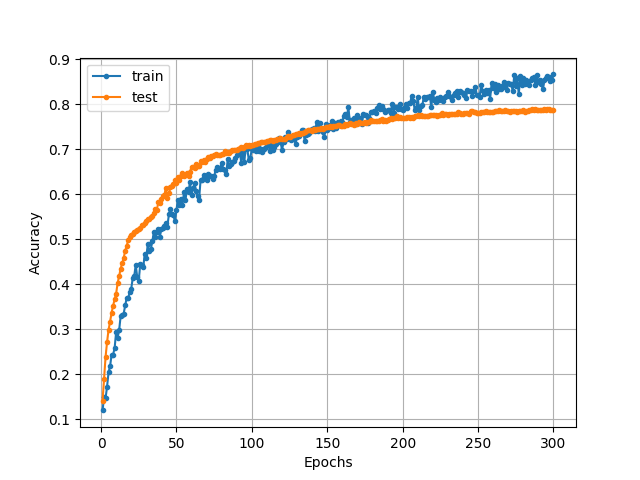
<ドロップアウトありのときの分類精度の推移>
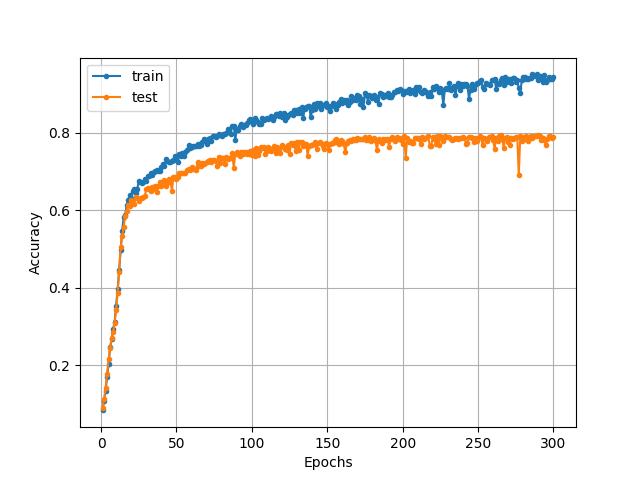
<ドロップアウトなしのときの分類精度の推移>
図から、ドロップアウトを適用したモデルは、ドロップアウトを適用しないモデルよりも、過学習を抑えられていることがわかります。
5.3 Early Stopping
Early Stoppingとは、その名の通り学習を早期に終了させてしまうというものです。つまり、過学習が起きる寸前 or 発生したらすぐに学習を終了させることで、ベストなモデルを手に入れようという試みになります。これにより、無駄な計算機リソースの消費防止にも繋がります。
5.3.1 KerasにおけるEarly Stoppingの適用方法
KerasにおいてEarly Stoppingは、keras.callbacks.EarlyStoppingにより定義されています。使い方は、fitメソッド内で、引数: callbacksに、EarlyStoppingを渡せばよいです。EarlyStopping関数の主な引数の説明は以下の表の通りです。
| 引数 | 説明 |
|---|---|
monitor |
何を基準に学習を早期終了させるかを指定します。 デフォルトは val_lossになっています。 |
patience |
何エポックの間、監視値: monitorに変化がないことを許容するかを指定します。 |
verbose |
学習中にEarlyStoppingが適用されたことを明示的に表示するかしないかを指定します。 デフォルトは0(表示しない)です。 |
Early Stoppingの簡単な適用例は以下のようになります。この例では、2エポックの間、テストデータに対する損失関数の値に改善が見られないと、学習が停止するように設定されています。
early_stopping = EarlyStopping(patience=2, verbose=1)
model.fit(x=x_train, y=y_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, y_test), callbacks=[early_stopping])
5.3.2 Early Stoppingの適用結果
5層ニューラルネットワークでEarly Stoppingの効果を検証したソースコードは、GitHubにcompare_early_stopping.pyとして置いてあります。
compare_early_stopping.pyを動作させた結果、以下のような図が得られました。
Output:
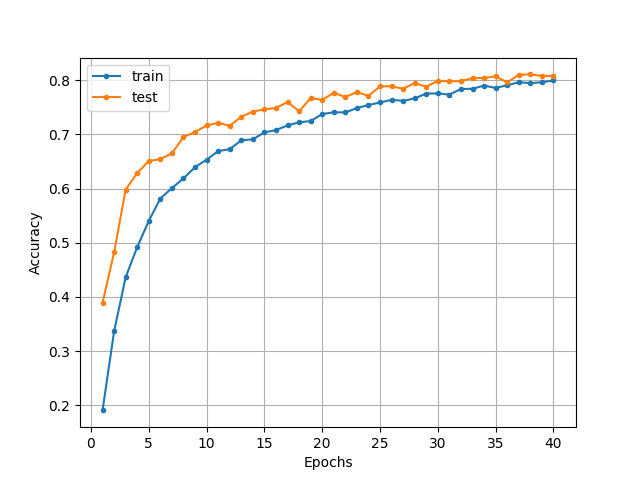
<Early Stoppingありのときの分類精度の推移>
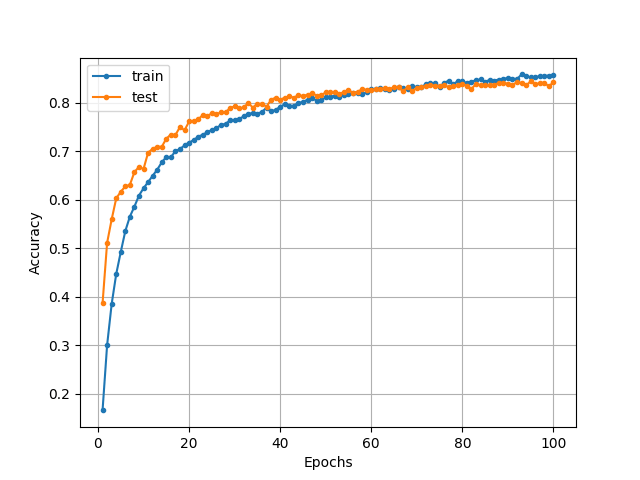
<Early Stopping無しのときの分類精度の推移>
図より、Early Stoppingを適用したときには、40エポックで学習が停止し、過学習している様子は読み取れません。一方で、Early Stoppingを適用しなかったときには、60エポックあたりから過学習の傾向が読み取れます。
まとめ
今回は様々な学習のテクニックについて、実際にKerasでモデルを実装し、その効果を検証してきました。次回は、畳み込みニューラルネットワークについて扱います。
なお、このシリーズは次回で完結予定です。
本稿で扱わなかったものの、ゼロから〜で紹介されている、「ハイパーパラメータの検証」については、今後「ハイパーパラメータの最適化 & 交差分割検証」をテーマに別の投稿で詳しく紹介する予定です!
ソースコード
ソースコードは、GitHubより入手できます。



