2020-06-06

不均衡データの分析

はじめに

機械学習を使った研究や実応用で避けて通れないのが、不均衡なデータセットを扱うことです．具体例としては，機械学習全般で言えば異常検知や，自然言語処理分野ではフェイクニュースの検知，音声処理分野では音声区間検出等，数え始めたらキリのないほどありそうな気がしてきます．

不均衡データを用いて機械学習モデルを学習させること自体は，通常の均衡データを用いるときとほぼ変わりない手順で実行できると思います．問題は「分析」です．モデルの学習がうまくいっているか，学習させたモデルが検証用データ・テストデータに対して有効であるかどうか，この二つをどのように確認するかが不均衡データを扱うときの鍵になってきます．そこで本稿の前半部分では，よく論文等で目にするメジャーな評価手法を掻い摘んで紹介します．後半部分では，不均衡データを扱う分類問題に実際に取り組み，その結果を前半部分で扱う評価手法に基づいて評価・分析することで，各指標についての理解を深めることを目指します．

1. 数値で評価

定量的な数値で評価するパターンとしては，精度 (Accuracy)・適合率 (Precision)・再現率 (Recall)・F1値 が代表的なものとして挙げられます．それに付随して，混同行列 (Confusion matrix) が用いられる場合もあります．何度も目にするこれらの評価指標ですが，念のため以下で定義とともに抑えておきます．

1.1　Accuracy

Accuracy は精度（正解した割合）なので，正解した数を全体数で割ることで求められます．

\begin{equation} \mathrm{Accuracy} = \frac{TP + TN}{TP + FP + TN + FN} \tag{1} \end{equation}

TP・TN・FP・FN の説明も以下に載せておきます．

  • TP (True Positive)
    予測結果も正解データもともに Positive なラベルが付与されているサンプル数
  • TN (True Negative)
    予測結果も正解データもともに Negative なラベルが付与されているサンプル数
  • FP (False Positive)
    正解データでは Negative と付与されているものの，予測結果は Positive であったサンプル数．FA (False Alarm) と呼ばれることもあります．
  • FN (False Negative)
    正解データでは Positive と付与されているものの，予測結果が Negative であったサンプル数．Miss と呼ばれることもあります．

　Accuracy の問題点

後ほど実験でも確認しますが，Accuracy は不均衡データの分析には向いていません．というのも，データセットのラベル分布が偏っていると，分子の正解数が多数を占めるクラスの影響を強く受けてしまうため，評価値が良くなってしまう傾向にあるからです．例えば，データセットのうち 80% が Positive で， 20% が Negative なラベルを持つとき，常に Positive を返す分類器の精度は 80% になります．一見すると，それなりに良いスコアに見えてしまいますね．

1.2　Precision

Precision は予測結果が Positive であったデータのうち，どの程度のデータが本当に Positive であるかを示す指標です．

\begin{equation} \mathrm{Precision} = \frac{TP}{TP + FP} \tag{2} \end{equation}

1.3　Recall

Recall は Positive なラベルを持つ正解データのうち，どの程度モデルが Positive と判定できたかを示す指標です．True Positive Rate (TPR) とも呼ばれます．

\begin{equation} \mathrm{Recall} = \frac{TP}{TP + FN} \tag{3} \end{equation}

1.4　F1値

F1値は Precision と Recall の調和平均 (harmonic mean) で求められます．Precision と Recall はトレードオフの関係にあると言われているので，その二つの調和平均を取ることで統一的にモデルの性能を評価しようという指標です．

\begin{equation} F_1 = 2 \times \frac{\mathrm{Precision} \times \mathrm{Recall}}{\mathrm{Precision} + \mathrm{Recall}} \tag{4} \end{equation}

F値には，$F_\beta$ という重みつきの派生版もありますが，ここでは扱いません．

1.5　Confusion Matrix

混同行列（Confusion Matrix）は，上述の TP・TN・FP・FN の4つの分類を表を使ってわかりやすく表現したものです．実際には表ではなくヒートマップが使われることがほとんどかと思います．混同行列の数値の見せ方には二通りあり，「サンプル数をそのまま表示するパターン」と，「TP と FN，TN と FP の組ごとに正規化をして表示するパターン」があります．どちらを使うかは，タスク次第といった所でしょうか．なお，以下の実験では両方とも出力しています．

2. 曲線の形状や面積で評価

続いて，曲線の形状やその曲線の作る面積の大きさで評価するパターンの紹介に移ります．代表的な指標としては，受信者動作特性曲線（Receiver Operating Characteristic Curve）と，Precision-Recall 曲線，Detection Error Tradeoff 曲線の3つがあります．

2.1　Receiver Operating Characteristic Curve

受信者動作特性曲線（ROC曲線）は，横軸に False Positive Ratio (FPR): $\frac{FP}{TN + FP}$ をとり，縦軸に True Positive Ratio (TPR): $\frac{TP}{TP + FN}$ をとる曲線です．予測結果が Positive か Negative かどうかを判断する閾値 (threshold) を $[0, 1]$ の範囲で少しずつずらして，各閾値における FPR と TPR を求めることで描画できます．ここで，閾値よりも大きい値を持つ予測結果は Positive とみなし，小さい値を持つ予測結果は Negative とみなします．

閾値が 0 に近いときは，ほとんどの予測結果が Positive であると判断されるので，TP と FP が大きくなり，TPR と FPR ともに 1 に近づきます．一方で，閾値が 1 に近いときは，ほとんどの予測結果が Negative であると判断されるので，TP と FP が小さくなり，TPR と FPR は 0 に近づきます．

閾値の範囲は，$[0, 1]$ に限りませんが，深層学習においてはシグモイド関数やソフトマックス関数を出力の関数として使うことが多く，これらの関数の値域は $(0, 1)$ であることから，ここでは $[0, 1]$ としています．

　Area Under Curve

ROC曲線と FPR (横軸) で囲まれた部分の面積を Are Under Curve (AUC) と言い，モデルの良し悪しを評価するのに用いられます．AUC の最大値は 1 で 最小値は 0.5 になります．AUC は 1 に近づけば近づくほど良く，0.5 はランダム分類を意味します．

　ROC-AUC の注意点

ROC曲線はモデルがベースライン（ランダム分類）よりも有意に分類ができているかどうかを直感的に確認するのに適していますが，次に紹介する Precision-Recall 曲線 (PR曲線)よりも不均衡データへの反応が鈍い傾向にあります．つまり，あまり正確に分類できなかったケースでも，AUC がそれなりに大きくなることがあります．この場合，モデル間比較が難しくなってしまうので，PR-AUC も併用した方が良いです．

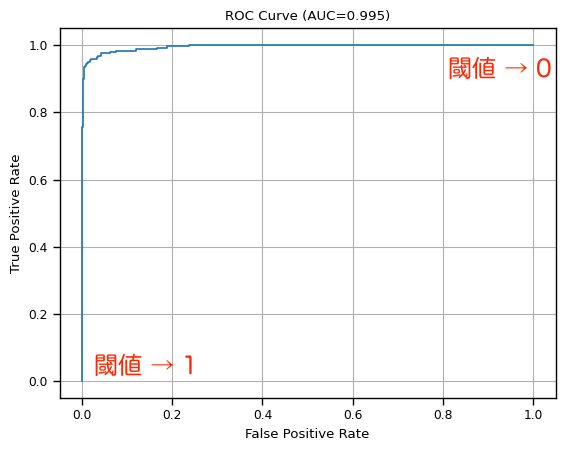
ROC曲線の例
図：ROC曲線の例

2.2　Precision-Recall Curve

Precision-Recall Curve (PR曲線) は，横軸に Recall を取り，縦軸に Precision をとった曲線です．描画の手順はROC曲線と全く同じです．閾値が 0 に近いと FN の数が減り，TP と FP の数が増加するので，Precision はノイズ (FP) が増えるため悪化し，Recall はノイズ (FN) が減るので改善します．他方，閾値が 1 に近づくと FP は小さくなり，FN が大きくなることから，Precision は改善し，Recall は 悪化します．

　Area Under Curve

ROC曲線と同様に曲線の作り出す面積が1に近いほど良いモデルと言えます．ただし下限は 0.5 ではなく，0です．なお実験では AUC の計算に，Average Precision (AP) を活用しています．

参考: （AP - Wikipedia）

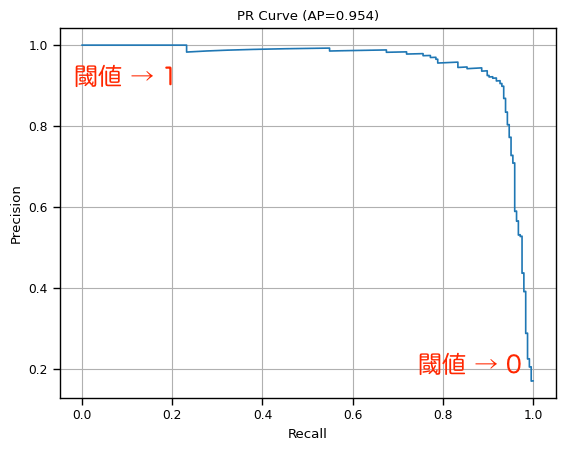
PR曲線の例
図：PR曲線の例

2.3　Detection Error Tradeoff Curve

Detection Error Tradeoff Curve (DET曲線) は，どの程度モデルが誤検知・未検知したかを分析するのに向いている指標です．若干マイナーな曲線ですが，音声処理等の分野で活用されています．DET曲線は横軸に False Positive Rate (FPR): $\frac{FP}{TN + FP}$ をとり，縦軸に False Negative Rate (FNR): $\frac{FN}{TP + FN}$ を取ります．FPR は False Alarm Rate (FAR) とも呼ばれ，FNR は Miss Rate と表記されていることもあります．なお描画の仕方は上述の2曲線と同じく，閾値を少しずつずらして対応する FPR と FNR をプロットしていく形です．

誤検出率：FPR も， 未検出率：FNR もできる限り小さくするのが目標となるので，DET曲線は原点に近づけば近づくほど良い傾向であるといえます．

　Equal Error Rate

Equal Error Rate (EER) は，FPR と FNR が等しくなる点 (値) を指します．EER は小さければ小さいほど良いモデルであると言える指標です．

誤検出も未検出も同程度重要視している場合には，EER に対応する閾値をモデルの閾値として使うという手もありかもしれません．しかし DET曲線 と， EER はデータの偏りを考慮していないので，不均衡データを扱う際にEERをベースに閾値を決めるのは注意が必要です．この場合，FPR と FNR の各重要度を考慮したコスト関数を設定すれば，ベストな閾値を求めることができると思います．

もしそのまま EER から逆算した閾値を使うと，Precision か Recall のいずれかが極端に良くなり，もう片方が極端に悪くなるという現象が発生すると予想されます．

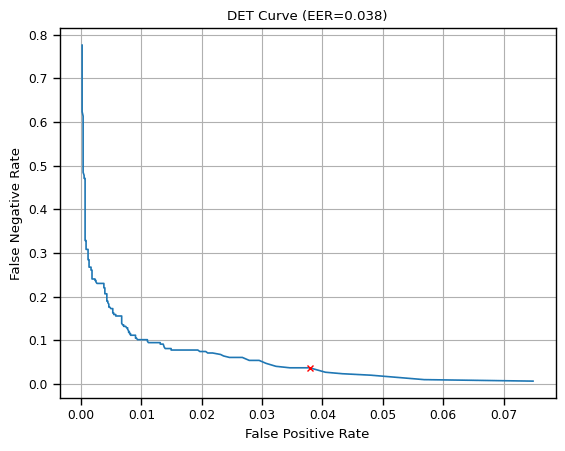
DET曲線の例
図：DET曲線の例（赤点は EER）

3. 簡単に実験してみる

一通り評価指標を見てきたところで，簡単な分類問題を扱って各指標の見え方の違いについて確認していきます．

3.1　問題設定

今回は MNIST データセットを活用して，入力画像（数字）が偶数か奇数かを判定するタスクに取り組みます．前処理としてデータセットに付与されているラベル (0-9) を偶数奇数 （偶数: 1，奇数: 0）に張り替え，わざと偶数ラベルを持つデータを減らすことで不均衡データセットに仕立て上げます．

3.2　モデル

モデルは隠れ層を2層（256・128次元）持つ，シンプルな順伝播型ニューラルネット (FFNN) にしました．実装には，PyTorch をメインで使い，評価指標等の計算には一部 scikit-learn を使っています．実装は，GitHub にて公開してあります．

　損失関数に重み付け

単に不均衡データセットを分類する Toy Problem だと面白味に欠けるので，Binary cross-entropy loss の Positive クラスに対応する項に重み付けをして，その振る舞いを実験で観察することにします．具体的には次の式(5)のような損失関数になります．

\begin{equation} \mathcal{L}_{\rm WBCE} = - \frac{1}{N} \sum_i^{N} w_{\rm pos}y_i \log (p(x_i)) + (1 - y_i) \log (1 - p(x_i)) \tag{5} \end{equation}

$N$: サンプル数，$y_i$: $i$ 番目のサンプルの正解ラベル，$x_i$: $i$ 番目のサンプルの入力データ，$p(x_i)$: 入力データ $x_i$ が モデルによって Positive であると判断される確率 (= シグモイド関数の出力)，$w_{\rm pos}$: Positive クラスの重み．

重み $w_{\rm pos}$ は，Negative ラベルを持つデータ数 $n_{\rm neg}$ を Positive ラベルを持つデータ数 $n_{\rm pos}$ で割った値: $\frac{n_{\rm neg}}{n_{\rm pos}}$ として求められます．

今回のタスクの場合，重み付けがない状態だと，偶数データの分類にミスをしてもデータ数が少ないため，損失関数にそこまで大きな影響を及ぼしません．一方で重み付けをした状態で偶数データの分類にミスをすると，奇数データの分類にミスをしたときよりも大きなペナルティを被るので，モデルが不均衡データの性質をより意識できるようになると期待されます．

3.3　実験結果

実験結果は，均衡状態での結果，不均衡状態での結果，不均衡状態で損失関数に重み付けを行ったときの結果の3つに分けて紹介します．

　偶数データ減量前

均衡状態での MNIST データセットを使った偶数奇数の分類性能は，次の表のようになりました．軒並み良い数値を出しているのを見ると，簡単なタスクだったようです．

表：均衡状態での MNIST データセットの偶数・奇数分類結果
データ Accuracy Precision Recall F1 AUC AP EER
Validation 0.983 0.986 0.980 0.983 0.998 0.997 0.016
Test 0.987 0.989 0.984 0.986 0.998 0.998 0.014


　偶数データ95%減量後

続いて偶数ラベルを持つデータを元の5%まで減らしたときの結果を見ていきます．比較用に訓練用データのラベル分布に基づいてランダムに分類を行う分類器の結果を Random として載せました．

表：不均衡状態での MNIST データセットの偶数・奇数分類結果
データ / モデル Accuracy Precision Recall F1 AUC AP EER
Validation 0.985 0.946 0.719 0.817 0.996 0.933 0.024
Test 0.988 0.955 0.780 0.859 0.996 0.958 0.020
Random 0.915 0.056 0.053 0.054 0.505 0.047 NA

偶数データの減量前の結果と比較すると主に次の3点が読み取れます．

  • Accuracy と AUC があまり変化していない．
    これは評価指標の説明時に紹介した傾向がそのまま現れたものです．Accuracy と AUC は，多数派を占める Negative（奇数）ラベルを持つデータの分類結果に強く影響されがちなので，奇数データの分類が上手く行っていればそれなりに高いスコアがでてしまいます．特に Accuracy はランダム分類でも 0.915 とかなり高いスコアが出てしまっています．

  • 減量後の Recall と F1 が悪化している．
    混同行列 (Confusion Matrix) を見ればわかりやすいのですが，この実験では，偶数ラベルを持つデータの分類にかなり失敗しています．（28% の偶数データが誤分類されています．）そのため，偶数ラベルが付与されているデータの正解率を示す，Recall の値も悪化したと考えられます．また F1 は Precision と Recall の調和平均なので，どちらかが悪化するとそれに伴って悪化します．

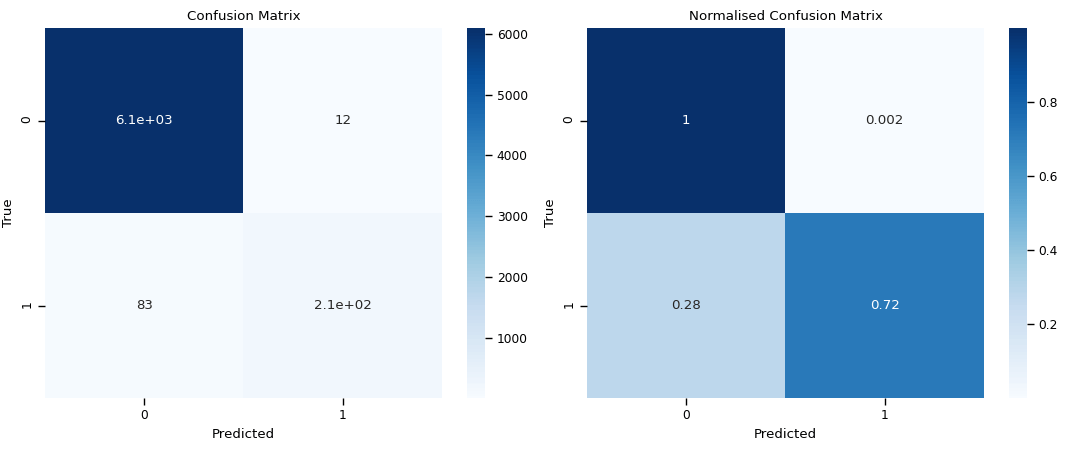
検証用データを用いたときの混同行列
図：検証用データを用いたときの混同行列
  • 減量後の AP と EER に悪化の傾向が見られる．
    ROC-AUC とは異なり，AP は Recall の大幅な悪化を見逃さず，きちんと数値に反映しています．EER についても，0.6% から 0.8% 程度の悪化が見られます．


　損失関数に重み付け後

最後に損失関数を式(5)に置き換えたときの分類結果を見ていきます．明らかな違いとしては，Precision が悪化した代わりに，Recall が大幅に改善したことが挙げられます．ただし，その他の指標は同程度か若干悪化しています．したがって，モデルが偶数ラベルを持つデータをより意識できるようになったものの，その分ノイズ (誤検出) が増えてしまったと言えます．

更に言えば，閾値を調整すれば損失関数に重み付けをしなくても類似の結果を再現することができると思われるので，果たしてこのタスクにおいて損失関数への重み付けに意味があるのかどうかは謎です．

表：不均衡状態での MNIST データセットの偶数・奇数分類結果
（損失関数に重み付けあり）
データ Accuracy Precision Recall F1 AUC AP EER
Validation 0.985 0.781 0.942 0.854 0.996 0.938 0.024
Test 0.983 0.777 0.890 0.830 0.991 0.914 0.049
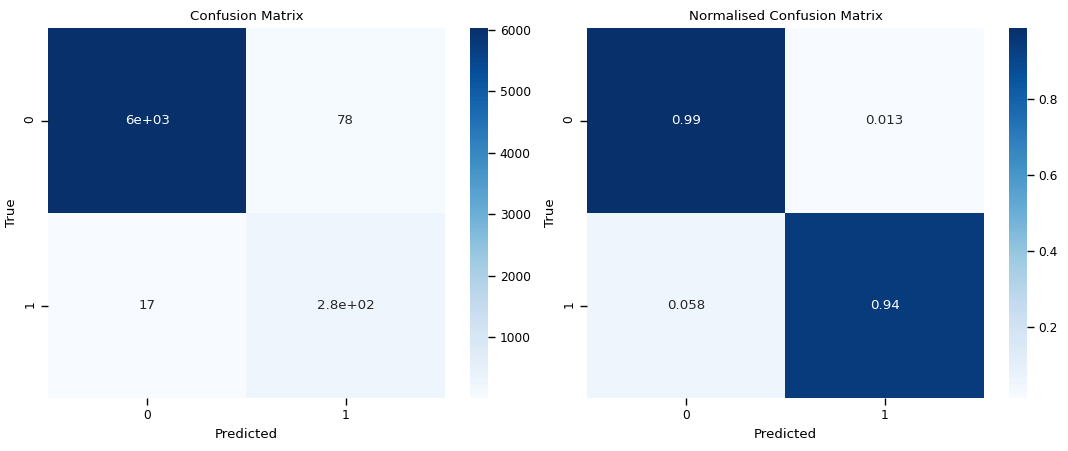
検証用データを用いたときの混同行列
図：検証用データを用いたときの混同行列（損失関数に重み付けあり）

まとめ

本稿では種々の評価指標について一通り確認し，簡単な分類問題を通して各指標の振る舞いの違いを観察しました．実装は GitHub にて公開してあります．お気軽にご利用ください．

チェックポイントのセーブは行わない仕様になっているので，研究等に活用する際はくれぐれもご注意ください．